로그 변환
[ 목적 ]
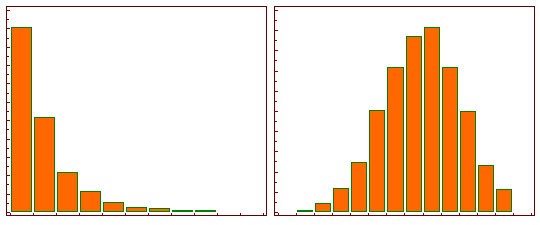
정규 분포가 아닌 실제 데이터를 정규분포로 변환해주기 위해 로그를 사용.
(정규분포 : 평균, 중앙값 및 최빈값은 동일한 값을 가지며, 평균과 분산이라는 두 개의 매개 변수로 정의)
[ 설명 ]
로그는 통계 모델링 및 통계 분석에서 필수적인 도구.
X는 y 의 거듭제곱에 대한 b와 같기 때문에 X의 기저 b- 로그가 y 와 같은 밑 (b)에 대해 로그를 정의
(X = b ʸ이므로 log (X) = y)
- 밑이 2 : 2³ = 8이므로 8의 밑이 2 인 로그는 3입니다.
- 밑이 10 : 10² = 100이므로 밑이 10 인 100의 로그는 2입니다.
- 자연 로그 : 자연 로그의 밑은 수학 상수 "e"또는 2.718282와 같은 오일러 수
따라서 7.389의 자연 로그는 2입니다. e² = 7.389
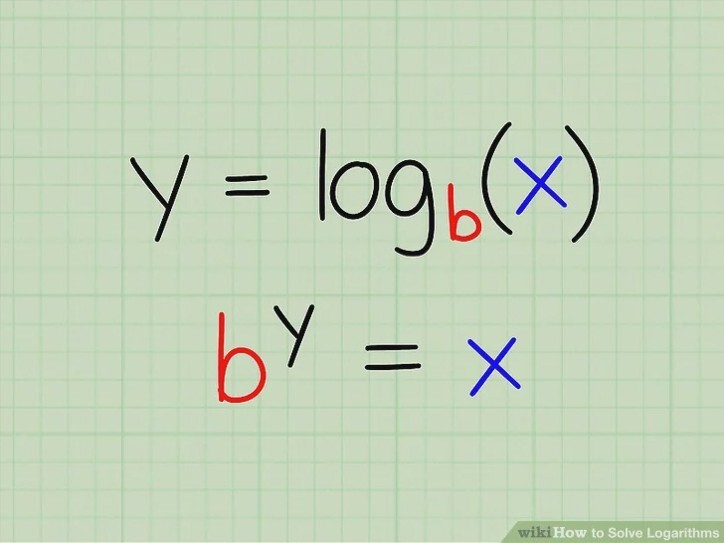
[ 적용 ]
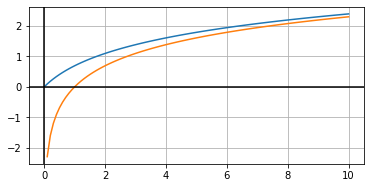
실제 로그함수 log (X) = y는 아래와 같이 나타남.
문제는 x가 일 때, y가 마이너스 무한대로 수렴하는 부분.
ax.plot(x, np.log1p(x))
ax.plot(x, np.log(x))
[ 로그함수 특징 ]
- 0<x<1 범위에서는 기울기가 매우 가파릅니다.
즉, x의 구간은 (0,1)로 매우 짧은 반면, y의 구간은 (−∞,0)으로 매우 큽니다. - 따라서 0에 가깝게 모여있는 값들이 x로 입력되면, 그 함수값인 y 값들은 매우 큰 범위로 벌어지게 됩니다.
즉, 로그함수는 0에 가까운 값들이 조밀하게 모여있는 입력값을 넓은 범위로 펼칠 수 있는 특징을 가집니다. - 반면, x값이 점점 커짐에 따라 로그함수의 기울기는 급격히 작아집니다.
이는 곧 큰 x값들에 대해서는 y값이 크게 차이나지 않게 된다는 뜻이고 이에 따라서 넓은 범위를 가지는 x를 비교적 작은 y값의 구간 내에 모이게 하는 특징을 가집니다. - 그렇기에 결과적으로 데이터의 분포를 모았을 때 밀집되어 있는 부분은 퍼지게
퍼져있는 부분은 모아지게 만들 수 있는 것입니다.
위와 같은 특성 때문에 한쪽으로 몰려있는 분포에 로그 변환을 취하게 되면 넓게 퍼질 수 있습니다.
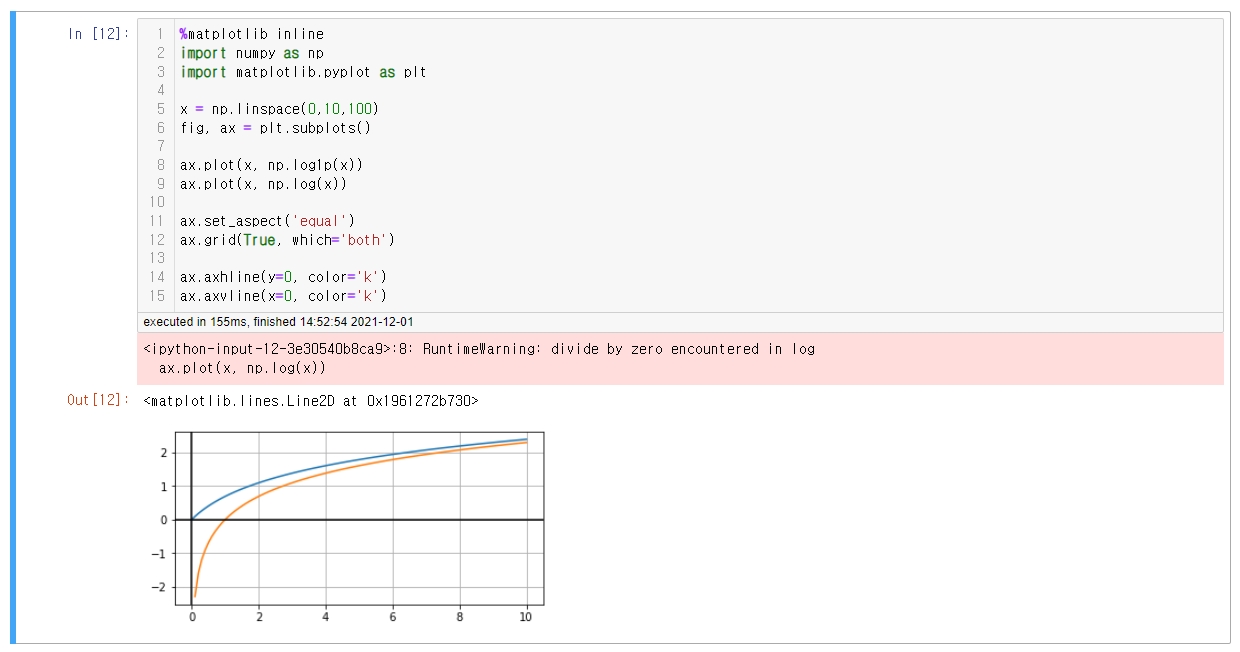
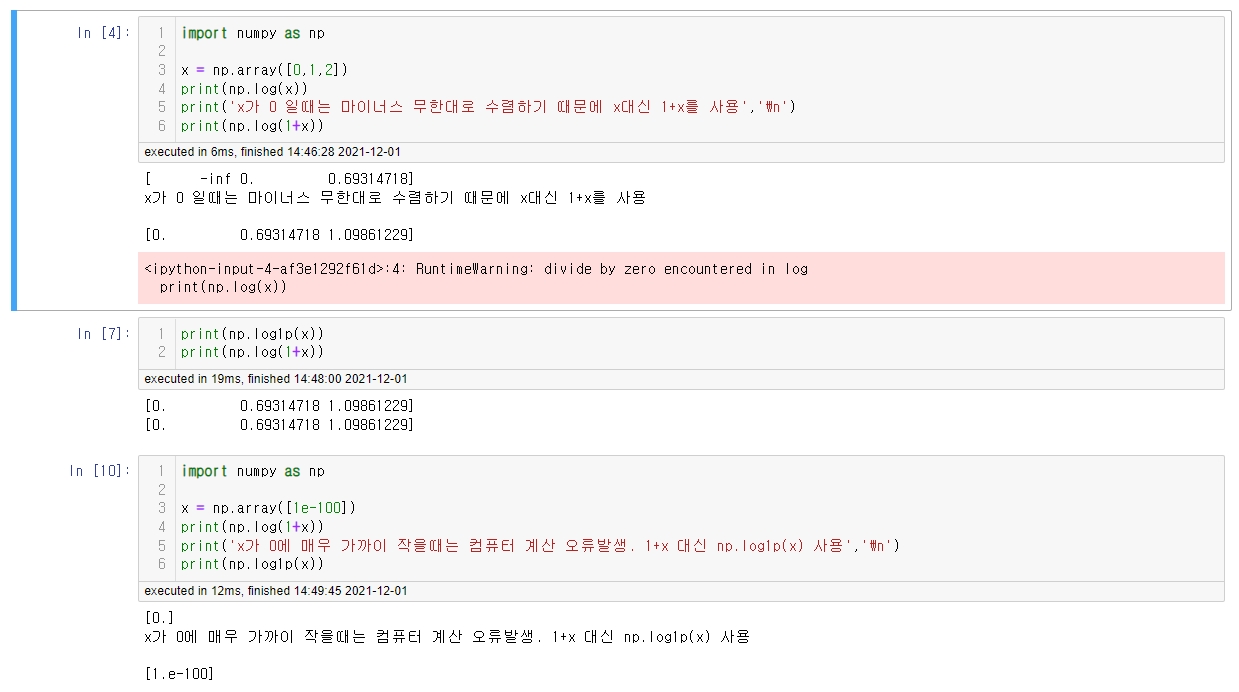
np.log()가 아닌 np.log1p()인 이유
x =0 일 경우, 마이너스 무한대 값을 가짐
x+1을 해줌으로써 x = 0 ->1의 값을 가지고
따라서 y= 마이너스 무한대 -> 0의 값을 가짐
np.log(1+값) = np.log1p() 동일
But,
변환 전 값이 매우 작은 경우
컴퓨터 계산의 오류가 생기기 때문에
직접 +1을 해주는 것이 아닌 np.log1p()을 사용
'빅데이터(Big Data) 이론과 코드 > 2. 데이터 전처리' 카테고리의 다른 글
| 홈런볼 매출 데이터 분석 Bar Chart Race (2) | 2023.02.05 |
|---|---|
| Pandas Dataframe 조건에 맞게 값 변경 하기 (2) | 2022.03.04 |
| [zip 함수] 파이썬 내장함수 zip() (0) | 2022.03.03 |


